Background

LiDAR is an established technology that is increasingly being used to derive spatial stand metrics, which is increasing the accuracy and efficiency of operational forest inventory. Since the first application of LiDAR in forestry almost three decades ago (Nelson et al. 1984), the technology has been widely used to quantify spatial variation in stand height, basal area (Watt 2005; Means et al. 1999), diameter, volume (Næsset 1997), canopy properties (Næsset and Okland 2002) and species composition (Donoghue et al. 2007). The strength of LiDAR lies in its ability to provide accurate distance information and to penetrate the canopy, thereby providing information on both the horizontal and vertical distribution of vegetation structure.

As stem volume is a key determinant of forest value, the use of LiDAR to provide an unbiased and accurate estimate of this stand dimension is of considerable interest to forest managers. Volume is typically determined from inventory measurements that are often time-consuming and expensive. Metrics derived from LiDAR have been shown to exhibit moderate to strong relationships with stem volume across a range of different coniferous species (Næsset 1997; Means et al. 2000), demonstrating the potential of LiDAR for inventory purposes. Compared to traditional inventory, with only plot-based measurements, LiDAR has a number of potential advantages that include increased fine scale spatial resolution, lower costs and increased precision (Næsset 2002; Holmgren and Jonsson 2004).

Field inventory costs increase markedly with plot size, and LiDAR costs increase with pulse density. Consequently a key issue requiring investigation is how far these elements can be reduced without compromising precision of the regression between LiDAR metrics and volume. Development of accurate LiDAR height metrics are reliant on an accurate digital terrain model (DTM) as the canopy returns must be converted from elevation above sea-level to height above the DTM. However, once an accurate DTM has been obtained it should be possible to reduce the pulse density for the estimation of volume.

The influence of pulse density on the precision of relationships between stand and LiDAR metrics has been widely investigated. In stands dominated by Norway spruce (Picea abies (L.) Karst.) and Scots pine (Pinus sylvestris L.), Gobakken and Næsset (2008) found that point densities could be reduced from 1.13 point to 0.25 points m-2 with little effect on the quality of inventory results. In a mixed conifer forest, where pulse densities were reduced from 9 to 0.01 pulses m-2, it was found that correlations between LiDAR metrics and key stand metrics (tree height, diameter at breast height, and total basal area) were relatively unaffected until pulse densities were reduced below 1 pulse m-2 (Jakubowski et al. 2013). In mixed conifer-hardwood stands, it was found that pulse density could be reduced from 3.2 to 0.5 pulses m-2 with little effect on the precision of relationships between LiDAR and stand metrics (Treitz et al. 2012).

Fewer studies have investigated how plot size and the interaction between pulse density and plot size influence the precision of regressions between field measurements and canopy metrics. In general the homogeneity of canopies in even-aged forests allows for reductions of plot sizes to 0.02 ha, without substantial deterioration of the LiDAR-volume relationships (Gobakken and Næsset 2008). There are, however, substantial differences in this homogeneity between different forest types that may necessitate variation in plot sizes to accommodate this. This homogeneity ranges from high (in very dense unthinned planted stands with few gaps) through moderate (in thinned planted stands with greater ground area) to low (in natural forests).

Research is required that investigates how plot size and pulse density influence the quality of LiDAR-volume relationships across planted forest stands that include a wide variation in stand densities. Ideally, other important factors that influence estimation of canopy metrics, such as the laser system, flight specifications, data characteristics and data processing steps should be maintained constant to mitigate their influence. The characteristics described were part of a recently acquired LiDAR dataset that sampled the entire extent of New Zealand’s predominantly Pinus radiata D. Don (radiata pine) resource. Using this dataset, the objective of this research was to investigate how pulse density and plot size influence the precision of LiDAR metric-volume relationships.

Methods

Dataset used

The dataset used was from a national inventory of planted forests (LUCAS) undertaken to measure and monitor temporal change in national carbon stocks. This inventory was undertaken by New Zealand as part of its obligations under the Kyoto Protocol and the United Nations Framework Convention on Climate Change (Beets et al. 2010). This dataset has been fully described previously (Beets et al. 2012; Stephens et al. 2012; Stephens et al. 2007).

In stands established after 1 January 1990, circular plots with an area of 0.06 ha were installed between June and September 2008 using a regular systematic 4 km grid. In stands established prior to 1990, plots of 0.06 ha were installed during 2010 on an 8 km grid. Field plot centres were located using a 12-channel differentially corrected global positioning system (GPS) to within ± 3 m.

The LiDAR survey was undertaken aerially using a Cessna 207 aircraft in February 2008 (for pre-1990 forests) and 2010 (for post-1989 forests) using a small footprint (~0.20 m) Optech ALTM 3100EA system integrated with a Rollei AIC digital camera. The LiDAR settings used to achieve first-return pulse densities of at least 3 returns m-2 are summarised in Table 1. The system also utilised an Applanix 510 Position and Orientation System (POS) that uses GPS and inertial measurement unit (IMU) sensors, and a GPS-based computer controlled navigation system.

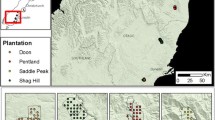
Table 1 Summary of key LiDAR settings for the dataset collected
Full size table

From this dataset, LiDAR metrics and stand information for 374 plots were extracted for the analysis. These data were taken across a range of plantation species that included plot representation of the following species: 350 plots (94%) in Pinus radiata, 13 plots (3%) in Pseudotsuga menziesii var menziesii (Mirb.) Franco (Douglas-fir), 7 plots (2%) in Eucalyptus nitens H.Deane & Maiden (shining gum), and the remaining four plots within stands with minor species. The distribution of these plots is shown in Figure 1.

Figure 1
figure 1

Distribution of plot locations used for the modelling.

Full size image

Diameter at breast height (dbh) was recorded for each plot tree. A sample of at least 16 trees per crop type (i.e. silvicultural regime, age, species etc.) within each plot also had height measured. A plot-specific height-diameter relationship was used to determine height of any remaining trees in the plot. The bearing and distance from each tree to the plot centre was recorded. Stand slope was measured using an inclinometer and defined as the average of the maximum gradient at the plot centre and the gradient at ninety degrees to that.

Within the dataset there was a wide range in stand and LiDAR metrics (Table 2). Stand density ranged from 17 – 2283 stems ha-1 which exceeds the normal operational range found within planted forests in New Zealand. Total stem volume ranged from 0.048 to 1020 m3 ha-1. LiDAR metrics also ranged widely with most variation noted in the 30th height percentile which ranged 51-fold from 0.6 to 30.7 m (Table 2).

Table 2 Summary statistics describing the dataset
Full size table

Processing of LiDAR and field data

Following the method described in Gonzalez Aracil (2011), which uses the equations described in Goulding (1995), individual tree volumes were determined from diameter and measurements (or estimations) of height. Summation of these volumes yielded a plot level estimate of total stem volume. Measurements of distance and bearing allowed total stem volume to be recalculated under a range of plot sizes. Where the plots were on sloping ground, a slope-corrected radius was used (Hayes 2005), both for the original plots and the simulated reduced size plots.

Terra-Scan software was used to classify ground and non-ground returns using the algorithm described by Axelsson (2000). Manual identification of breaklines by skilled operators was undertaken to improve DTM quality. These classified ground returns were used to construct a DTM by connecting them into a Triangulated Irregular Network (TIN), and then linearly interpolating them onto a regular grid. Pulses were extracted individually from the data and assimilated using the raw coordinates. The DTM grid size was 1 m, but linearly interpolated to the exact horizontal return location for more accurate ground characterisation.

LiDAR data were extracted for each plot assuming a circular plot shape. Although field plots were often elliptical, previous research demonstrates the assumption of circularity to have little effect on values for key LiDAR height metrics (<0.22%) within this dataset (Adams and Pont 2012). LiDAR metrics extracted for the analysis included the 30th, 70th and 95th height percentiles, mean height and canopy cover (percentage of returns from above a cut-off of 0.5 m to remove the understorey) as these are widely used for development of volume equations. The described LiDAR metrics were generated from all returns.

Thinning of LiDAR dataset

For the unthinned dataset (plot size = 0.06 ha; pulse density = 4 returns m-2) the best model describing total stem volume was,

V = α H m + β
(1)

where V is the total stem volume (m3 ha-1), Hm is the mean LiDAR height (m), and α, β are the regression coefficients, which had respective values of 28.02 and -76.45. This relationship had a R2 of 0.77. Addition of further variables to this model did not substantially improve model accuracy.

Models of V were developed under a wide range of plot size and pulse densities using the independent variable (Hm) described in Equation 1. LiDAR metrics were thinned to 84 different pulse densities ranging from 4 pulses m-2 to 0.01 pulses m-2 for plot sizes ranging from 0.01 to 0.06 ha (in 0.005 ha intervals). The raw data was thinned to remove a specified proportion of pulses (and all corresponding returns). Each iteration removed a random set of pulses from the original dataset, so successive thinnings would not contain the same pulses.

Statistics were extracted for two sets of simulations. In the first set, coefficients in the volume equation were refitted for each pulse density/plot size combination. In the second set, coefficients in the volume equation were fixed at those used for the highest plot size (0.06 ha) and pulse density (4 pulses m-2). For both sets of simulations, the coefficient of determination (R2) was obtained for each pulse density/plot size combination. For plot size/pulse density combinations in the first simulation the percentage variation in coefficients of the regression equation was determined as the mean percentage change in each of the two regression coefficients, compared to their original values (for a plot size of 0.06 ha and pulse density of 4 returns m-2).

Results

Influence of pulse density on model precision

For the first set of simulations, where coefficients were allowed to vary, the model performance (R2) remained relatively constant in response to reductions in pulse density until values were reduced below 0.5 pulses m-2 (Figure 2). Following this there was a marked decline in R2. The coefficients in the regression were almost constant above 1 pulse m-2 (varying by less than 0.4%), and only varied by more than 5% for the β coefficient (see Equation 1) with pulse densities less than 0.25 pulses m-2 (Figure 3). This stability was also apparent in the very low variation in model precision between simulations with fixed and varying coefficients. Differences in the coefficient of determination (R2) between the two simulations, for a given pulse density, did not exceed 10-15.

Figure 2
figure 2

Relationship between pulse density and the coefficient of determination (R2) for simulations where a fixed plot size of 0.06 ha was used.

Full size image
Figure 3
figure 3

Relationship between pulse density and percentage variation in coefficients of the regression equation (described in Eqn. 1 ) for simulations where a fixed plot size of 0. 06 ha was used.

Full size image

Influence of plot size and pulse density on model precision

For the first set of analyses where the coefficients were allowed to vary, the coefficient of determination (R2) exhibited little change from the base value of 0.77 for plot sizes greater than 0.03 ha where the pulse density exceeded ca. 0.1 pulses m-2 (Figure 4). As long as pulse densities were maintained above 0.1 pulses m-2, reductions in plot size to 0.01 ha resulted in only moderate losses in R2 of up to ca. 0.03 (from ca. 0.77 to 0.74). Similarly, at plot sizes exceeding 0.025 ha, pulse densities could be reduced to 0.01 pulses m-2, with only moderate losses in R2 to 0.60 (Figure 4). As pulse densities declined below 0.1 pulses m-2 within plots of less than 0.025 ha, there was a sharp decline in R2 reaching values as low as 0.48 in plots of 0.01 ha with pulse densities of 0.01 pulses m-2 (Figure 4).

Figure 4
figure 4

Relationship between coefficient of determination (R2) for the volume equation and plot size and pulse density. Values are shown as a checkerboard plot (top) and as a 3D surface (bottom). The colour scale shows variation in R2 for the volume equation.

Full size image

At pulse densities exceeding 0.5 pulses m-2, coefficients in the volume function were very stable across plot sizes greater than 0.04 ha, exhibiting less than 1% variation from the base coefficients (Figure 5). The average variation of coefficients was never more than 13% for all plots greater than 0.03 ha under pulse densities greater than 0.01 pulses per m2. There was a marked increase in average coefficient variation at very low pulse densities that was particularly pronounced as plot sizes declined below 0.025 ha (Figure 5).

Figure 5
figure 5

The relationship between mean percentage variation in regression coefficients for the LiDAR volume equation and plot size and pulse density. Values are shown as a checkerboard plot (top) and 3D surface (bottom). The colour scale shows percentage variation in regression coefficients.

Full size image

Findings were very similar for simulations run with regression coefficients fixed at values found for the highest plot size (0.06 ha) and pulse density (4 pulses m-2). These simulations show a very similar decline in R2 to those where parameters were refitted (i.e. Figure 4), with absolute differences in R2 not exceeding 10-15. As R2 values for these simulations were indistinguishable from those in Figure 4 these data are not shown.

Regression of the number of pulses per plot against model precision integrated the effect of the plot size and pulse density, described previously. The coefficient of determination did not markedly decline until a threshold value of 100 pulses per plot was reached (Figure 6).

Figure 6
figure 6

The relationship between the coefficient of determination ( R 2 ) of the volume equation and number of pulses per plot, with values on the x - axis plotted using a linear scale (top) and log scale (bottom).

Full size image

Discussion

The results from this study are broadly consistent with previous research investigating the effects of plot size and pulse density on precision of relationships between LiDAR and canopy metrics. Most studies have found that LiDAR pulse densities can be reduced to between 0.06 – 0.5 pulses m-2 with little consequent effect on precision of canopy metrics (Goodwin et al. 2006; Næsset 2004a; Gobakken and Næsset 2008; Treitz et al. 2012; Jakubowski et al. 2013). Similarly, previous research has shown that reductions in plot size are possible to 0.02 ha without negative impacts on the precision of regressions between LiDAR metrics and volume (Gobakken and Næsset 2008).

This study extends previous research by examining the combined effect of plot size and pulse density on model precision. When these two variables were examined in combination, little deterioration in the precision of the volume function was noted for plot sizes greater than 0.03 ha where the pulse density exceeded ca. 0.1 pulses m-2. Analyses indicate that the number of pulses per plot integrates the effect of these two factors, with little change in the precision of the volume function until a threshold of 100 pulses per plot is reached. Once this point is reached there are too few pulses to enable the calculation of robust LiDAR metrics. The volume equation was found to be stable across most pulse density and plot size combinations. The effect of data thinning on R2 hardly varied between simulations where the parameters were held constant or allowed to change.

The relatively low sensitivity of model precision to pulse density demonstrated in this study has implications for the cost effectiveness of LiDAR as an inventory tool. Currently most LiDAR is acquired within forests at a pulse density of between 1–2 pulses m-2 in New Zealand (New Zealand Aerial Mapping pers. comm.). Reduction of the pulse density to well below these levels, under situations where an accurate DTM is available, would markedly increase the cost efficacy of LiDAR as a tool for describing spatial variation in canopy metrics.

In an operational setting, pulse density and LiDAR acquisition cost can be reduced through flying faster, reducing the swath overlap or flying at higher altitude. Increases in aircraft speed or a reduction in the swath overlap will reduce the pulse density without influencing other specifications such as footprint diameter and ability of the laser to penetrate the canopy (Magnusson et al. 2010).

In contrast, flying at a higher altitude affects several features of the data. The footprint diameter and swath width increases while the reflected energy, ability of the laser to penetrate the canopy, and maximum pulse repetition frequency decline (Magnusson et al. 2010). As a result of these changes flying at higher altitude results in a change in the distribution of echo categories, an upward shift in the canopy-height distribution and a lower proportion of multiple returns (Goodwin et al. 2006; Næsset 2004b, 2009). Although changes to these features do not significantly affect the precision of regression equations for common stand metrics, such as height and stand volume, coefficients in the regression equations are likely to change between acquisitions at different altitudes (Næsset 2004b, 2009).

Conclusions

This study demonstrates the relative insensitivity of precision in LiDAR-derived models of volume to changes in plot size and pulse density. Little change in R2 was noted until data were reduced to plot sizes of 0.03 ha and pulse densities of 0.1 pulses m-2. Simulations where model parameters were fixed yielded almost identical results to those where parameters were refitted to each combination of plot size/pulse density. Acquisition of LiDAR data at lower pulse densities will markedly improve the cost-effectiveness of this technology for inventory purposes.